2021年東京都

解答

問１は解説参照

問２①は解説参照、②$\frac{48}{5}cm^2$

解説・解き方の例

問１

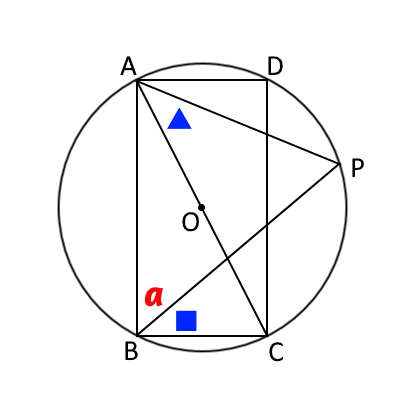
図で▲と■は円周角により等しい。

また、$a$と■は合わせて直角なので、$a+■=90°$である。

よって、$\angle PAC=(90-a)°$となる。

---

問２①

$\triangle QRPが二等辺三角形$であることを証明するには、通常は二辺が同じ長さか、二角が同じ大きさか、のどちらかである。

この場合は「2角が同じ大きさである」ことであろうと目星をつけ、さらに下図の▲と■が同じなのであろうと予想する。

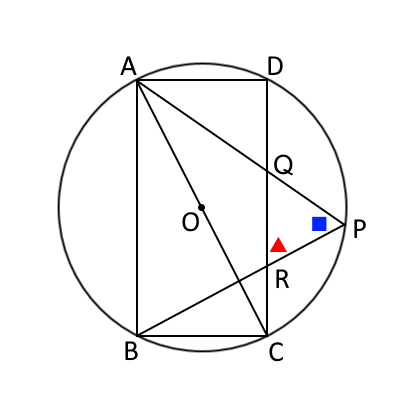
下の図で、▲と◎は対頂角が等しい。また、$\triangle ABP$が二等辺三角形なので■と★は底角で等しい。そして、$AD$と$DC$が平行（$ABCD$が長方形なので）なので、★と◎は錯角により等しい。よって、■＝★＝◎＝▲となり、$\triangle QRP$は二等辺三角形であることが証明された。

---

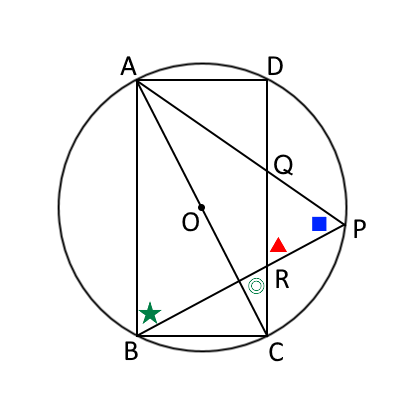
問２②

$\triangle PRC$とは、下図のオレンジ色の三角形である。

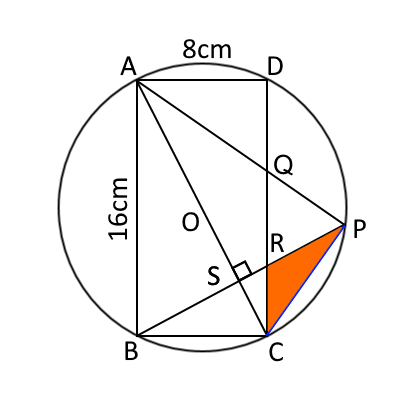
問題をとき始める前に、必要な情報を整理しておく。（証明略）

$AC$と$BP$の交点を$S$とすると、

• $AB=AP$より、$AS⊥BP$である。
• $ABCD$は長方形なので、$\angle ABC$、$\angle BCR$は直角である。
• $\triangle BSC≡\triangle PSC$である。
• $\triangle ABC∽\triangle BSC$$∽\triangle BCR∽\triangle CSR∽\triangle CSP$である（すべて相似）。

したがって、これらの情報を利用して、$SR:RP$がわかれば、$\triangle PRC$の面積がわかるであろうと目星をつける。

$SC:SR=AB:BC=2:1$より、$SR=\frac{1}{2}SC$となる。

$SC:SP=BC:AB=1:2$より、$SP=2SC$となる。

よって、$SR:SP=\frac{1}{2}SC:2SC=1:4$である。よって、$SR:RP=1:3$である。

これにより、$\triangle PRC$の面積は$\triangle PSC$すなわち、$\triangle BSC$の$\frac{3}{4}$であることがわかった。

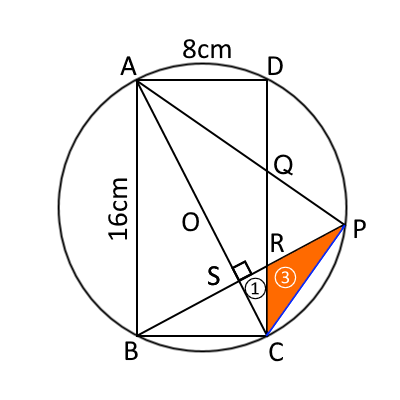
同様に考えると、$AS:SC=2BS:\frac{1}{2}BS=4:1$なので、$\triangle BSC=\frac{1}{5}\triangle ABC$である。

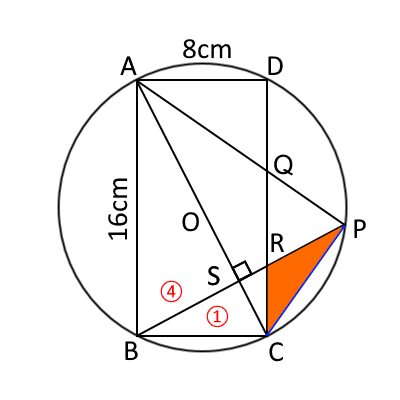
よって、$\triangle PRC=$ $\triangle BSC\times \frac{3}{4}=$ $\triangle ABC \times \frac{1}{5} \times \frac{3}{4} = $ $\triangle ABC \times \frac{3}{20}$となる

$\triangle ABC=16 \times 8 \times \frac{1}{2}=64$より、$\triangle PRC=64 \times \frac{3}{20}=\frac{48}{5}$となる。

---

★豆知識

下図のように、直角三角形$\triangle ABC$の$A$から$BC$に垂線$AD$を下ろすと、 直角三角形が二つできる（$\triangle ABD$と$\triangle CAD$）

このとき、線分比$AB:AC=x:y$とすると、線分比$BD:DC=x^2:y^2$になり、 面積比$\triangle ABD:\triangle CAD=x^2:y^2$になる。

問題

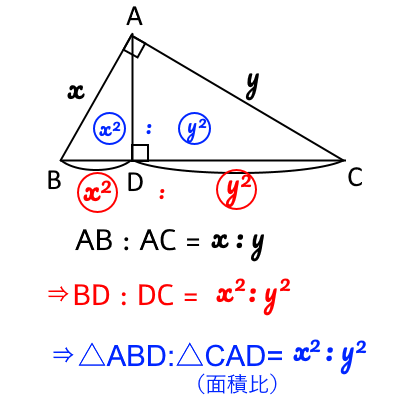
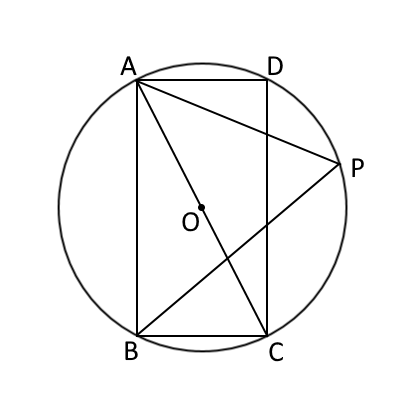
図１

図１で、四角形$ABCD$は$AB \gt AD$の長方形であり、点$O$は、線分$AC$を直径とする円の中心である。

点$P$は頂点$A$を含まない弧CD上にある点で、頂点$C$、頂点$D$のいずれにも一致しない。

頂点$A$と点$P$、頂点$B$と点$P$をそれぞれ結ぶ。このとき次の問に答えなさい。

問１：$\angle ABP=a°$とするとき、$\angle PAC$の大きさを表す式を書きなさい。（実際の問題では選択問題である）

---

問２：次の図２は、図１において、辺$CD$と線分$AP$との交点を$Q$、辺$CD$と線分$BP$との交点を$R$とし、$AB=AP$の場合を表している。

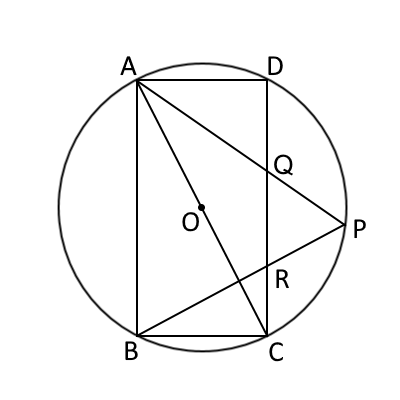
図２

①$\triangle QRP$は二等辺三角形であることを証明せよ。

②頂点$C$と点$P$を結んだ場合を考える。$AB=16 cm, AD=8 cm$のとき、$\triangle PRC$の面積を求めなさい。